Algunas preguntas muy recurrentes entre la gente que apenas empieza a jugar o que ni siquiera ha jugado aún rol son: ¿Cómo funcionan los dados? ¿Para qué sirven los dados?
La respuesta más habitual incluye, entre otros razonamientos, que añade el factor de aleatoriedad o suerte que por naturaleza hay en cualquier acción. Esto es, por ejemplo, por mucho que una persona sea muy buena tocando el laúd puede ponerse nerviosa y desafinar. Entonces, ¿Dónde se ve reflejado cómo de bueno eres en algo?, eso sería el bonificador que sumas a esa tirada aleatoria, tal que, si tienes un bonificador muy alto habrá menos probabilidades de que falles.
Queda pues a la vista que se trata de un juego de probabilidades basado en tiradas de dados; es decir, un juego de matemáticas. Y es que, sin tratar de asustar a nadie, la mejor forma de entender el porqué de los dados es hacer unos pequeños cálculos.
Los Dados en la Creación de Personajes
A la hora de empezar una campaña de rol, lo primero que hacemos es crear un personaje y nos encontramos que, de acuerdo al manual, nuestros stats se deciden aleatoriamente tirando cuatro dados de seis de los cuales sumamos los tres valores más altos. Preguntas: ¿Por qué dados de seis?¿Por qué este sistema tan raro de tirar cuatro y escoger los tres más altos?
Para contestar a estas preguntas la primera observación es: si sumamos el resultado de tres d6 tenemos que el mínimo resultado posible es 3 = 1+1+1 y el máximo es 18 = 6+6+6. Como sabemos, las puntuaciones de un aventurero pueden tomar un valor máximo de hasta 20, siendo 18 la puntuación mas alta que una persona suele alcanzar (tal y como dice el manual). Teniendo en cuenta que podemos sumar hasta dos puntos extra a alguna característica según la raza y nuestra primera observación, tenemos que de esta forma nuestros stats siempre van a quedar dentro de los limites por lo que, a priori, parece un método razonable. Pero no solo eso, es la única combinación de dados que cumple esto y al mismo tiempo mantiene la uniformidad (Cada combinación de números tiene la misma probabilidad de ocurrir).
Por otro lado, la esperanza (el valor esperado o media) en una tirada de dado de seis caras es 3,5 y de ahí, la esperanza de la suma en una tirada normal de tres dados sería 10,5. Según el manual, 10-11 es el promedio para un humano por lo que, de nuevo, parece que todo funciona correctamente. Sin embargo, también añade lo siguiente: "... los aventureros y muchos monstruos están por encima del promedio en la mayoría de características." Es aquí donde entra el efecto del cuarto dado.
Supongamos que lanzamos tres dados y en uno de ellos sacamos un uno. Al lanzar el cuarto dado tenemos una alta probabilidad de sacar algo mejor que ese uno y por tanto mejorar la suma final. En general, podemos interpretarlo de esta forma; partiendo de todas las posibles combinaciones de tiradas de tres dados, el cuarto dado siempre va a mejorar o mantener la suma, nunca a empeorarla. Y es que, si calculamos la esperanza de lanzar cuatro dados y sumar los tres valores mas altos, tenemos que, a diferencia del lanzamiento normal de tres dados, esta es 12 (truncando los decimales). Y no solo eso, si no que, la probabilidad de que obtengamos un valor por encima de lo esperado para una persona promedio (10) es del 73%. De esta forma, jugamos con la probabilidad para fomentar que nuestros aventureros sean más formidables que una persona de a pie.
Por todo esto, es por lo que se utilizan dados de seis caras y el método descrito. Está claro que no eligieron este método por casualidad.
Un D20 para casi todo
Si te has leído el manual o ya has jugado algo de D&D, habrás podido comprobar que todos los Checks se hacen siempre con una tirada de dado de veinte caras. Y es que cada sistema de rol se construye alrededor de un tipo de dado; en el caso de Dragones y Mazmorras es el d20.
Cuando queremos golpear, realizar alguna actividad o resistir algo; hacemos una tirada con la intención de superar un cierto valor (la armadura del oponente, un rango de dificultad definido por el master...), teniendo en cuenta la suma de bonificadores que tengamos a la actividad, tal y como mencionamos al comienzo. Entonces, si llamamos 'dr' al resultado del dado en la tirada, 'bn' al bonus que tengamos y 'min' al mínimo que debemos alcanzar, lo que buscamos es que dr + bn ≥ min, o lo que es lo mismo, dr ≥ min - bn. Si ahora quisiéramos calcular la probabilidad de éxito en el check, solo tendríamos que ver que en un dado de veinte caras, 21-(min - bn) es la cantidad de números en el dado por encima o igual a ese valor y por tanto:
Nótese que cualquier resultado negativo será automáticamente probabilidad 0 e igualmente cualquiera por encima de uno será automáticamente 1 (Hay que multiplicar por 100 para obtener el resultado en porcentaje).
Llegados a este punto ya sabemos cómo calcular nuestra probabilidad de superar un check, veamos entonces un poco cómo funcionan estas probabilidades frente a las dificultades definidas en el manual. Según las reglas, se definen las siguientes clases de dificultad: 5 muy fácil, 10 fácil, 15 moderado, 20 difícil, 25 muy difícil y 30 casi imposible.
Supongamos que tenemos un personaje que debe superar un check en una habilidad para la cual no tiene competencia (proficiency) y tiene un +0 en esa característica. Esto es, un personaje haciendo una tarea para la cual no destaca por encima de la media y para la cual además no ha practicado, entrenado o similar. En esta situación tenemos que su probabilidad de éxito para realizar una tarea fácil será del 55%, mientras que superar una dificultad difícil o muy difícil será algo imposible para él en cualquier circunstancia. Es coherente, ¿No?
En cambio, supongamos ahora que otro jugador quiere realizar la misma tarea, pero en este caso se trata de un personaje con un bonus de +5, que además tiene competencia, supongamos de +2 (Nivel del 1 al 4). Esto es, un personaje que destaca sobresalientemente en esa tarea y que además es algo a lo que esta acostumbrado. En este caso, automáticamente superara una dificultad muy fácil, con una probabilidad del 90% superara la dificultad fácil, con un 65% de probabilidad podrá superar una moderada, con un 40% una difícil, con un 15% una muy difícil y le resultara imposible superar una de casi imposible hasta subir de nivel lo suficiente (Como mínimo nivel 13 siendo 5% su probabilidad). De nuevo tenemos que las probabilidades, con las características descritas, se acercan a lo que seria el azar de una acción en la realidad y podemos concluir que el sistema de clases de dificultad que nos ofrece el manual es muy acertado.
Tiradas Enfrentadas
Cuando realizamos una tirada enfrentada contra la de otro individuo, lo que queremos es superarla. Por lo tanto, el mínimo a superar será el resultado final del oponente más uno. Esto es, una vez sabemos el resultado del rival, podemos usar la fórmula anterior para calcular nuestra probabilidad de ganarle sumando uno a su resultado. Sin embargo, ¿podemos saber en general que probabilidad hay de superar al contrario? La respuesta es sí, veamos cómo.
Para poder estudiar nuestra probabilidad de ganar el enfrentamiento necesitamos definir nuevas variables para el contrincante. Llamemos 'drc' al posible resultado del dado rival y 'bnc' al bonus que este tenga para la tirada. Por un lado tenemos que cada posible valor que puede obtener tiene una probabilidad de 1/20 de ocurrir y por otro tenemos que nuestra probabilidad de superarlo, como hemos comentado antes, es (21 - ((drc + bnc + 1) - bn)) / 20 = (20 - (drc + bnc - bn)) / 20. De aquí obtenemos que la probabilidad de que el oponente saque un valor concreto y nosotros superemos ese mismo valor es: (20 - (drc + bnc - bn)) / 400 (El producto de ambas).
Finalmente, si sumamos nuestra probabilidad de ganar para cada posible resultado del rival, tenemos que nuestra probabilidad general de ganarle es:
Por ejemplo, si un jugador con un bonus total de +5 en Engaño trata de estafar a otro con un bonus total de +0 en Perspicacia, su probabilidad de conseguirlo será del 72%. Si por el contrario, un personaje con +0 en Engaño trata de estafar a otro con +5 en Perspicacia, su probabilidad en general de conseguirlo en una tirada enfrentada será del 22%. Y es que, si nos fijamos, la formula depende únicamente del bonus de cada jugador que participa en el enfrentamiento, es decir, lo que entra en juego es la habilidad real de cada individuo para ganar al otro.
Ventaja, Desventaja e Inspiraciones
Al hacer una tirada con ventaja, desventaja o inspiración, lanzamos dos dados y elegimos el mejor o peor resultado según qué aplicamos. Está claro que para cada dado independientemente tenemos la misma probabilidad de éxito, pero en conjunto, ¿Qué probabilidad tenemos de lograr el éxito?
En el caso de la desventaja, al elegir el peor resultado, con que uno de los dados no sea un éxito nuestra tirada será un fracaso o lo que es lo mismo, necesitamos que ambos dados nos den un éxito para no fallar. Como los dados son independientes entre sí podemos simplemente multiplicar las probabilidades de cada uno y tenemos que:
En el caso de la inspiración y la ventaja elegimos el mejor resultado. Por eso, la única opción que tenemos de fallar es que ninguno de los dados de la tirada nos dé un éxito. Como de nuevo los dados son independientes (podemos directamente multiplicar probabilidades) y la probabilidad de fracaso es siempre uno menos la de éxito, y viceversa, tenemos que:
Ahora que tenemos las formulas de probabilidad para la ventaja y la desventaja, podemos estudiar de nuevo qué pasa con las clases de dificultad.
Un personaje que debe superar un check en una habilidad con desventaja (o ventaja) para la cual tiene un bonus de +5 y que además tiene competencia, supongamos de +2, tendrá unas probabilidades de: 100% para superar una dificultad de muy fácil, con un 81% (o 99%) superará la dificultad fácil, con un 42% (o 87%) de probabilidad podrá superar una moderada, con un 16% (o 64%) una difícil, con un 2% (o 27%) una muy difícil y le resultara imposible superar una de casi imposible en ambos casos.
En un análisis superficial, comparando con las probabilidades que teníamos para la tirada sin ventaja ni desventaja, podemos decir que aplicar una de estas condiciones es cercano a añadir o disminuir un nivel de dificultad a la tirada, pero sin perder o ganar en ningún caso la posibilidad de superar el check. Y es que, por muy bien que se te de una actividad si te están molestando mientras la realizas es normal que te cueste más de lo habitual y, por el contrario, que te sea más fácil si te ayudan.
El resto de Dados
Ahora que hemos visto el uso del D20 cabe preguntarse qué pasa con el resto. Los D4, D6, D10 y D12 en D&D se usan para calcular la vida de los personajes y el daño tras impactar. Así pues, en esta parte lo que queremos es encontrar una forma de calcular la vida y el daño medio que tendría un personaje con ciertas características.
En ambos casos funciona similar, partimos de un tipo de dado que lanzamos un cierto número de veces, sumamos todos los valores obtenidos, añadimos el bonus propio y eso se corresponde con nuestra vida o daño. La clave para calcular el valor medio esperado reside entonces en cuántos dados estamos usando y de qué tipo son. Como tenemos que la esperanza en un dado equilibrado de 'm' caras siempre es (m + 1) / 2, el valor esperado para la suma de valores de un lanzamiento de 'n' dados de 'm' caras será n (m + 1) / 2. Visto esto el trabajo esta casi hecho.
En el caso de la vida tenemos que, según nuestra clase, se nos asigna un tipo de dado. Por nivel que subamos en la clase, nuestra vida se incrementa según el resultado de dicho dado más nuestro bonificador de constitución. Podemos calcular nuestra vida esperada teniendo en cuenta que:
- A nivel uno nuestra vida es el valor máximo del dado más el bonus de constitución.
- Los incrementamos de nuestra característica de constitución actúan con carácter retroactivo sobre la vida que sumábamos en los niveles previos.
En el caso del daño ocurre similar, dependerá directamente del ataque que estemos realizando, y simplemente tendremos que sumar el valor esperado para cada tipo de dados y el bonus que nos indique el ataque. Por ejemplo, si un paladín con un bonus de fuerza de +3 ataca con una espada larga a dos manos (1d10 + Fuerza) usando Castigo Divino a nivel 1(2d8), el daño esperado será:
((10+1) / 2) + 3 + (2·(8+1) / 2) = 5,5 + 3 + 9 = 17,5
Estos valores no tienen un paralelismo directo con la realidad, podríamos comparar el daño producido por distintas armas y ver si es coherente. Sin embargo, hay que entender que son meras representaciones numéricas del daño que causamos o que somos capaces de soportar. Dentro del juego veremos que, saber calcular vida media y daño medio será útil para el diseño de monstruos, entre otros.
Conclusiones
Con esto concluimos nuestro estudio sobre el uso de los dados en D&D 5e.
El azar en un sistema de rol es necesario para representar la variabilidad que existe en la realidad al realizar cualquier acción. Aunque uses la misma receta, el bizcocho a veces sabe distinto.





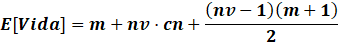
Muy interesante! Mola ver un estudio de la aleatoriedad en los roles desde un punto de vista más matemático.
ResponderEliminar